Question

Which graph represents the function y = 2x – 4? A coordinate plane with a line passing through (negative 4, 0) and (0, 2). A coordinate plane with a line passing through (0, negative 4) and (4, negative 2). A coordinate plane with a line passing through (0, negative 4) and (2, 0). A coordinate plane with a line passing through (negative 4, 0) and (negative 2, 4).

Answer 1

The third option: "A coordinate plane with a line passing through (0, negative 4) and (2, 0)."

Explanation:

Use the equation defined by the function: y = 2x - 4 to check the (x, y) values they give you. If they both render true mathematical statements, those are indeed points on the plane that belong to the given line.

For the third case; the pairs (0,-4) and (2,0), both satisfy the equation of the line that is given.

For (0,-4): y = 2x - 4 becomes:

`(-4)=2(0)-4\\-4=0-4\\-4=-4` which is a TRUE statement

For (2,0): y = 2x - 4 becomes:

`(0)=2(2)-4\\0=4-4\\0=0` which is also a TRUE statement.

This option is the only one that verifies both given points as truly being part of the given line.

Answer 2

Answer: The correct option is

(C) A coordinate plane with a line passing through (0, negative 4) and (2, 0).

Step-by-step explanation: We are given to select the option that represents the following function :

`y=2x-4~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

Now, we know that the equation of a line passing through two points (a, b) and (c, d) is given by

`y-b=(d-b)/(c-a)(x-a).`

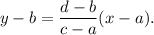
Option (A) : The line passing through the points (-4, 0) and (0, 2) is

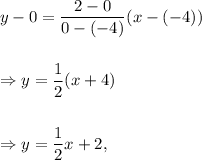`y-0=(2-0)/(0-(-4))(x-(-4))\\\\\\\Rightarrow y=(1)/(2)(x+4)\\\\\\\Rightarrow y=(1)/(2)x+2,` not same as equation (i).

So, option (A) is NOT correct.

Option (B) : The line passing through the points (0, -4) and (4, -2) is

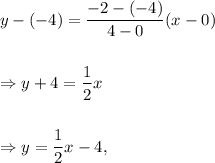`y-(-4)=(-2-(-4))/(4-0)(x-0)\\\\\\\Rightarrow y+4=(1)/(2)x\\\\\\\Rightarrow y=(1)/(2)x-4,` not same as equation (i).

So, option (B) is NOT correct.

Option (C) : The line passing through the points (0, -4) and (2, 0) is

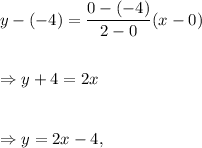`y-(-4)=(0-(-4))/(2-0)(x-0)\\\\\\\Rightarrow y+4=2x\\\\\\\Rightarrow y=2x-4,` which is same as equation (i).

So, option (C) is CORRECT.

Option (D) : The line passing through the points (-4, 0) and (-2, 4) is

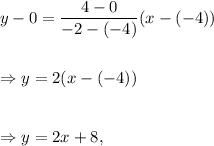`y-0=(4-0)/(-2-(-4))(x-(-4))\\\\\\\Rightarrow y=2(x-(-4))\\\\\\\Rightarrow y=2x+8,` not same as equation (i).

So, option (D) is COT correct.

Thus, the correct option is (C).