Answer: 490 N
Step-by-step explanation:
The complete question is:
Suppose you have to move a heavy crate of weight 875 N by sliding it along a horizontal concrete floor. You push the crate to the right with a horizontal force of magnitude 300 N, but friction prevents the crate from sliding.
What is the magnitude Fp of the minimum force you need to exert on the crate to make it start sliding along the floor? Let the coefficient of static friction
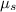 between the crate and the floor be 0.56 and that of kinetic friction,
between the crate and the floor be 0.56 and that of kinetic friction,
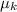 , be 0.47.
, be 0.47.
If we draw a free body diagram we will have the following:

This means:
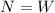 (1)
(1)
Where
 is the Normal force,
is the Normal force,
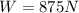 is the weight of the crate.
is the weight of the crate.
On the other hand, the Static Friction force
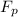 is:
is:
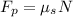 (2)
(2)
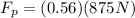
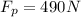 (3) This means the 300 N force exerted on the crate was not enough, because we need to push the crate to the right with at least 490 N to make the crate start sliding.
(3) This means the 300 N force exerted on the crate was not enough, because we need to push the crate to the right with at least 490 N to make the crate start sliding.
However, once the sliding motion begins we need to overcome the Kinetic Friction force
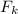 to keep the crate sliding at a constat velocity:
to keep the crate sliding at a constat velocity:
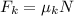 (4)
(4)

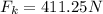 (5)
(5)