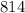Question

The nameplate on a 70 kVA transformer shows a primary voltage of 480 volts and a secondary voltage of 115 volts. We wish to determine the approximate number of turns on the primary and secondary windings. Toward this end, three turns of wire are would around the external winding, and a voltmeter is connected across this 3-turn coil. A voltage of 50 volts is applied to the 115 volt winding and the voltage across the 3-turn winding is found to be 0.77 volts. How many turns are there on the 480 V and 115 volt windings (approximately)?

Answer 1

Primary winding: 814 turns approximate.

Secundary winding: 195 turns approximate.

Step-by-step explanation:

Our main formula to find the number of turns for the primary and the secondary windings is the following:

`(V_(s) )/(V_(p)) =\frac{N{s}}{N{p}}`

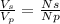
We already know the voltages, but we need to know at least one of the number of turns. We can get the number of turns of the secondary winding using the 3-turn coil and the voltages from the test (50 volts to the 115 volt winding and 0.77 volts found on the 3-turn winding), that is to say:

`(V_(test-coil) )/(V_(s)) =\frac{N{test-coil}}{N{s}}`

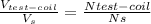
In this test, the secondary winding of the 70 kVA transformer acts as the primary winding. Keeping that in mind, we can find the number of turns for the secondary as follows:

`N_(s)=(N_(test-coil) xV_(s))/(V_(test-coil))` ⇒
`N_(s) =(3x50)/(0.77)`

`N_(s)`≈
`195`

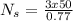
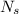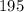
Now we can find the primary number of turns:

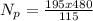
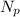`N_(p) = (N_(s)xV_(p))/(V_(s) )` ⇒
`N_(p) = (195x480)/(115)`

`N_(p)`≈
`814`