Question

A scientist has 40 liters of a 50% acidic solution. She adds a 20% acidic solution to create a mixture that has been diluted to

have 30% acidity. The graph models the percent of acidity in the final mixture.
20 40 60 80
How many liters of the 20% acidic solution should be added to create the needed 30% acidity in the final mixture?

A:0.5
B:30
C:80
D:37

Answer 1

Answer: C) 80 L

Explanation:

According to the dilution law,

`C_1V_1+C_2V_2=C_3V_3`

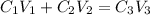
where,

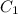`C_1` = concentration of acid solution = 50 %

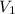`V_1` = volume of acid solution = 40 L

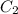`C_2` = concentration of another acid solution= 20%

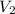`V_2` = volume of another acid solution= x L

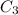`C_3` = concentration of resulting acid solution = 30 %

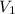`V_1` = volume of resulting acid solution = (40+x) L

Putting the values in the equation:

`50* 40+20* x=30* (40+x)`

`x=80L`

Thus 80 L of the 20% acidic solution should be added to create the needed 30% acidity in the final mixture.

Answer 2

C. 80 liters

Explanation:

A scientist has 40 liters of a 50% acidic solution. So, there are

`40\cdot 0.50=20\ liters`

of acid in this solution.

She adds x liters of 20% acidic solution to create a new mixture. In x liters of 20% acidic solution there are

`x\cdot 0.20=0.2x\ liters` of acid.

The total volume of the mixture is (40 + x) liters. This mixture has 30% acidity, so there are

`(40+x)\cdot 0.30=0.3(40+x)\ liters` of acid.

The amount of acid is the same, thus,

`20+0.2x=0.3(40+x)\\ \\200+2x=3(40+x)\ [\text{Multiplied by 10}]\\ \\200+2x=120+3x\\ \\2x-3x=120-200\\ \\-x=-80\\ \\x=80`