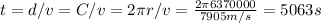Answer:
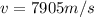
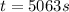
Step-by-step explanation:
A satellite is orbiting the earth just above its surface. The centripetal force making the satellite follow a circular trajectory is just its weight, so its centripetal acceleration is about 9.81 m/s2 (the acceleration due to gravity near the earth's surface). If the earth's radius is about 6370 km, how fast must the satellite be moving? How long will it take for the satellite to complete one trip around the earth?
The weight of the satellite is the centripetal force, so:

Which means:
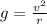
We can calculate then the velocity:
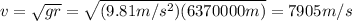
For calculating how long will it take for the satellite to complete one trip around Earth we consider that the distance of the trip is the circumference of the orbit. This is calculated as
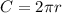 .
.
Since velocity is v=d/t, we have: