Question

Between t = 0 and t = t0, a rocket moves straight upward with an acceleration given by a(t) = A − Bt1 /2 , where A and B are constants. (a) If x is in meters and t is in seconds, what are the units of A and B? (b) If the rocket starts from rest, how does the velocity vary between t = 0 and t = t0? (c) If its initial position is zero, what is the rocket’s position as a function of time during this same time interval?

Answer 1

a) a= [m/s²] B = [m /
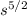`s^(5/2)`] b) v = A t - 2/3 B √t³

Step-by-step explanation:

The equation gives us for acceleration is a (t) = A - B √t

a) The unit of constants

Since the function is the acceleration and you have units of [m / s²] the quantities the right must have the same units, therefore, the counter A is in [m / s²] and the other term is B for the time

B t ½ = [m / s²]

B [s ½] = [m / s²]

B = [m / s²]
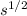`s^(1/2)`] = [m] / [
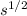`s^(1/2)` s²] = [m] / [
`s^(2+1/2)` ]

B = [m /
`s^(5/2)`]

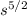b) To calculate the rocket speed we must use the definition of acceleration and integrate

a = dv / dt

dv = a dt

∫ dv = ∫ (A - B √t) dt

v = A (t) - B √t³ / 3/2

v = At ​​- 2/3 B √t³

We evaluated entered the initial point where the zero velocity equals a zero time and the final point with velocity v and time t

v = A t - 2/3 B √t³

c) To find the position we repeat the same proceeding for speed

v = dx / dt

dx = v dt

dx = / v dt

∫ dx = ∫ (A t - 2/3 B √t³ ) dt

x = At² / 2 - 2/3 B √t⁵ / 5/2

x = ½ A t² - 2/3 2/5 B √t⁵

Evaluating from the start point with zero position for a time of zero or to the end point with position x at time t

x = ½ A t² - 4/15 B √t⁵