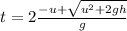Question

A ball is dropped with no initial speed from the height h above the plate. The plate is moving upward with constant speed u. Find the time interval between subsequent collisions of the ball with the plate. Neglect air resistance and assume that collisions are absolutely elastic. Acceleration of gravity is g.

Answer 1

Answer:
`t=2(-u+√(u^2+2gh))/(g)`

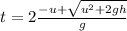
Step-by-step explanation:

Given

Ball is dropped from a height h and plate is moving upward with velocity u

considering plate at rest by providing a velocity in opposite direction thus ball is now moving with a velocity of u.

As acceleration is acting downwards therefore ball will accelerate with g

and time taken to collide with plate is

`h=ut+(gt^2)/(2)`

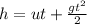
thus
`t=(-2u\pm √(4u^2+4* g* 2h))/(2g)`

Taking Positive value only

`t=(-2u+√(4u^2+4* g* 2h))/(2g)`

ball collide and bounces back to original height and then again collides with plate taking time=2t

Thus time between two collisions is equal to

`t=2(-2u+√(4u^2+4* g* 2h))/(2g)`

`t=2(-u+√(u^2+2gh))/(g)`