Question

Two gears in a machine are aligned by a mark drawn from the center of one gear to the center of the other. If the first gear has 24 teeth, and the second gear has 40 teeth, how many revolutions of the first gear are needed until the marks line up again?

Answer 1

5

Explanation:

for the first gear

revolutions/teeth

1 / 24

2 / 48

3 / 72

4 / 96

5 / 120

6 / 144

for the second gear

revolutions/teeth

1 / 40

2 / 80

3 / 120

4 / 160

the two marks will meet after 120 teeth, 5 revolutions of the first gear and 3 revolutions of the second.

the way to get that amount of teeth is

`24 = 2 * 2 * 2 * 3 = {2}^(3) * 3`

`40 = 2 * 2 * 2 * 5 = {2}^(3) * 5`

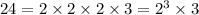
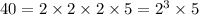
the Least Common Multiple equals the product of all factors, but those factors who are repeted for both numbers should be only once.

`{2}^(3) * 5 * 3 = 120`

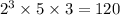
120 teeth are 5 revolutions for gear1 and 3 por gear2