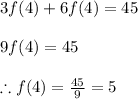Question

Suppose f and g are continuous functions such that g(4)=6 and lim x->4 [3f(x)+f(x)g(x)] = 45. Find f(4). ... (How do I begin solving this problem? Step by step assist please)

Answer 1

The value of f(4) is 5. We can write f(4) = 5.

Explanation:

Since it is given that

`\lim_(x\rightarrow 4)[3f(x)+f(x)g(x)]=45`

This is only possible if both the functions f(x) and g(x) are continuous at x = 4.

Now since the functions are continuous at x = 4 they need to be defined at the said value in accordance with the definition of continuous function.

Thus to obtain the limit we just put x = 4 in left hand side of the given relation thus getting

`[3f(4)+f(4)g(4)]=45..........(i)`

Now applying the given value of g(4) in equation 'i' we get

`3f(4)+6f(4)=45\\\\9f(4)=45\\\\\therefore f(4)=(45)/(9)=5`