First, it might be convenient to remind the definition of GCF. The GCF of two no-negative integers m,n, with
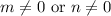 , is the largest positive integer that divides each of the integers.
, is the largest positive integer that divides each of the integers.
The algorithm of Euclides is a method to find the GCF of two numbers, which performs successive division. It starts by division of the smaller of the numbers into the larger, followed by the resulting remainder divided into the divisor of the each division until the remainder is equal to zero. Here, the algorithm stops and the GCF is the remainder of the previous division.
Now, let's compute the GCF(30,45).
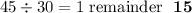
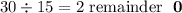
Since the remainder is zero, the algorithm stops and therefore, the GCF(30,45) is 15.