Question

A jet airliner moving initially at 612 mph (with respect to the ground) to the east moves into a region where the wind is blowing at 362 mph in a direction 15◦ north of east. What is the new speed of the aircraft with respect to the ground? Answer in units of mph.

Answer 1

966.22 mph

Step-by-step explanation:

Velocity of plane with respect to wind (Vp,w)= 612 mph east

velocity of wind with respect to ground, (Vw,g) = 362 mph at 15° North of

east

Write the velocities in vector form

`V_(p,w)=612\widehat{i}`

`V_(w,g)=362\left ( Cos15\widehat{i}+Sin15\widehat{j} \right )= 349.67\widehat{i}+93.69\widehat{j}`

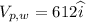
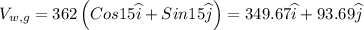
Use the formula for the relative velocity

`V_(p,w)=V_(p,g)-V_(w,g)`

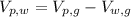
Where, V(p,w) is the velocity of plane with respect to wind

V(p,g) is the velocity of plane with respect to ground

V(w,g) is the velocity of wind with respect to ground

So,
`V_(p,g)=V_(p,w)+V_(w,g)`

`V_(p,g)=\left ( 612+349.67 \right )\widehat{i}+93.69\widehat{j}`

`V_(p,g)=961.67\widehat{i}+93.69\widehat{j}`

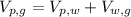
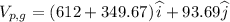
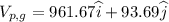
Magnitude of velocity of lane with respect to ground

`V_(p,g) = \sqrt{961.67^(2)+93.69^(2)}`

V(p,g) = 966.22 mph