Question

A spring-mass-spring system is hanging within a wall. One side of mass is having two springs in parallel of 1000 N/m and 3000 N/m. The other side of the mass is having one spring of 4000 N/m. Determine the equivalent stiffness.

Answer 1

The equivalent stiffness is 8000 N/m

Solution:

As per the question:

Refer to fig 1.

Two springs are connected in parallel on one side with spring constants:

K = 1000 N/m

K' = 3000 N/m

On the other side of the mass, one spring is attached with spring constant:

K" = 4000 N/m

The equivalent of the two spring is given by:

`K_(eq) = K + K' = 1000 + 3000 = 4000\ N/m`

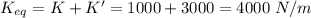
Now, the system is reduced to a two spring system with one spring attached to each side.

Refer to fig 2.

Both the springs are in parallel.

The equivalent stiffness is now given as the sum of the two springs as:

`K'_(eq) = K_(eq) + K`

Answer 2

`K_(eq) = 8000 N/m`

Step-by-step explanation:

Given data:

`K_1 = 1000 N/m,`

`K_2 = 3000 N/m`

`K_3 = 4000 N/m`

Equivalent of
`K_1 \ and K_2.`

`K_(eq) = K_1 + K_2`

`K_(eq) = 1000 + 3000`

`K_(eq) = 4000 N/m`

As we can see from figure both are parallel to each other therefore equivalent stiffness K is given as

K = 4000 + 4000

K = 8000 n/M

`K_(eq) = 8000 N/m`