Question

Show that, if n is an integer and n^3 + 5 is odd, then n is even, using:

a) contraposition

b) contradiction

Answer 1

Step-by-step explanation:

Let n be an integer

Given that
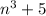`n^3+5` is odd

To prove that n is even

a) Proof by contraposition

Let
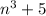`n^3+5` be non odd

Then this would be a multiple of 2 being even

`n^3+5 = 2m\\n^3=2m-5\\n^3=2(m-3)+1`

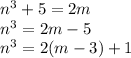
i.e. we get cube of n is odd since gives remainder 1 when divided by 2

It follows that n is odd.

Thus proved by contraposition

b) contradiction method:

If possible let
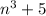`n^3+5` is odd for n odd.

Then we get

since n is odd,

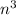`n^3` is odd being the product of three odd numbers

When we add 5, we get

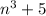`n^3+5` is even being the sum of two odd numbers

A contradiction

Hence our assumption was wrong

if n is an integer and n^3 + 5 is odd, then n is even