Question

Compute the thermal efficiency of a Rankine cycle with isentropic compression and expansion for which steam leaves the boiler as saturated vapor at 6 MPa and is condensed at 50 kPa.

Answer 1

Efficiency =30.4%

Step-by-step explanation:

A rankine cycle is a generation cycle using water as a working fluid, when heat enters the boiler the water undergoes a series of changes in state and energy until generating power through the turbine.

This cycle is composed of four main components, the boiler, the pump, the turbine and the condenser as shown in the attached image

To solve any problem regarding the rankine cycle, enthalpies in all states must be calculated using the thermodynamic tables and taking into account the following.

• The pressure of state 1 and 4 are equal

• The pressure of state 2 and 3 are equal

• State 1 is superheated steam

• State 2 is in saturation state

• State 3 is saturated liquid at the lowest pressure

• State 4 is equal to state 3 because the work of the pump is negligible.

Once all enthalpies are found, the following equations are used using the first law of thermodynamics

Wout = m (h1-h2)

Qin = m (h1-h4)

Win = m (h4-h3)

Qout = m (h2-h1)

The efficiency is calculated as the power obtained on the heat that enters

Efficiency = Wout / Qin

`Efficiency =( (h1-h2))/((h1-h4))`

first we calculate the enthalpies in all states

state 1

P=6000kpa x=quality=1

h1=2784kJ/Kg

s1=5.889KJ/kgK

state 2

entropy 1= entropy 2 P=50kPa

h2=2041kJ/Kg

state 3

P=50kpa x=quality=0

h4=h3=340.5kJ/Kg

then we use the efficiency ecuation

`Efficiency =( (h1-h2))/((h1-h4))=( (2784-2041))/((2784-340.5))=0.304`

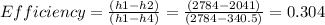
Efficiency =30.4%