Answer:
LAOD = 6669.86 N
Step-by-step explanation:
Given data:
width
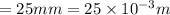
thickness
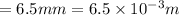
crack length 2c = 0.5 mm at centre of specimen
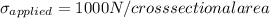
stress intensity factor = k will be
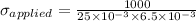
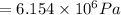
we know that
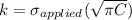
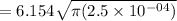 [c =0.5/2 = 2.5*10^{-4}]
[c =0.5/2 = 2.5*10^{-4}]
K = 0.1724 Mpa m^{1/2} for 1000 load
if
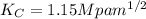 then load will be
then load will be
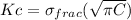
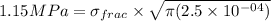

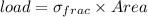
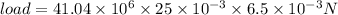
LAOD = 6669.86 N