Question

A product whose total work content time = 50 min is assembled on a manual production line at a rate of 24 units per hour. From previous experience with similar products, it is estimated that the manning level will be close to 1.5, uptime proportion will be 0.95, and line balancing efficiency will be 0.94. If 9 sec are lost from the cycle time for repositioning, determine (a) cycle time, (b) numbers of workers and (c) stations on the line.

Answer 1

a)Cycle time = 2.37 min

b)Numbers of workers =21

c)Stations on the line =24

Step-by-step explanation:

Given that

Total work content time(TWC) = 50 min

Production rate Rp= 24 units/hr

manning level will be close =1.5

Line balancing efficiency =0.94

a)

Cycle time

`T_c=(60E)/(R_P)`

`T_c=(60* 0.95)/(24)`

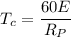
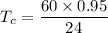
Cycle time = 2.37 min

b)

Numbers of workers ,W

`W=(TWC)/(T_c)`

`W=(50)/(2.37)`

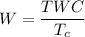
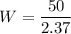
W= 21

Numbers of workers =21

c)

Stations on the line(n)

Lets find service time Ts

Ts = Cycle time - Time for repositioning

Ts = Tc- Tr

Ts= 2.37 - 9/ 60 min

Ts= 2.22 min

We know that efficiency

`\eta=(TWC)/(n.T_s)`

`0.94=(50)/(n* 2.22)`

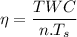
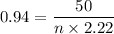
n=23.94 ⇒n=24

n=24

Stations on the line =24