Question

4. f(x) = 3x² – 21x² – 54x
Zero
Multiplicity
|
Effect​

Answer 1

x = 0 or x = -3

Explanation:

Solve for x:

-54 x - 18 x^2 = 0

Hint: | Factor the left hand side.

Factor x and constant terms from the left hand side:

-18 x (x + 3) = 0

Hint: | Divide both sides by a constant to simplify the equation.

Divide both sides by -18:

x (x + 3) = 0

Hint: | Find the roots of each term in the product separately.

Split into two equations:

x = 0 or x + 3 = 0

Hint: | Look at the second equation: Solve for x.

Subtract 3 from both sides:

Answer: x = 0 or x = -3

Answer 2

The zeros of the function are 0 and -3 and their multiplicity is 1.

Explanation:

The zeros refers to the values of the variable x for which f (x) = 0. Graphically, the zeros correspond to the abscissa (values of x) of the points where the parabola cut to the x axis. And the number of times the zeros is repeated as such is called a multiplicity of a zero.

To determine the behavior of a polynomial function with respect to the x axis (abscissa axis), we must factor the polynomial, f (x) = a (x - x1) (x - x2)… (x - xn-1) (x - xn)

The maximum degree of the polynomial in a polynomial function indicates the amount of zeros of a polynomial. In this case the maximum grade is 2, that is, this function has at most 2 zeros.

First we will make the corresponding calculations so that we have a single term of the same degree, taking into account that you cannot add or subtract two terms that have different degrees. In this way you can only group the terms that are similar and then add or subtract. So in this case you can only do the calculation 3*x²-21*x²

(3-21)*x²=-18*x²

As a result, you get the quadratic function:

-18*x²-54x=0

Now, to calculate the roots of this function, in this case, there are two methods:

First method

It consists in applying the formula
`\frac{-b+-\sqrt[2]{b^(2) -4*a*c} }{2*a}`

where a is the value that accompanies the term of degree 2 (in this case -18), b is the value that accompanies the term of degree 1 (in this case -54) and c is the value of the independent term of x (in this case case 0)

Replacing you get:

`\frac{54+-\sqrt{54^(2)-4*(-18)*0 } }{2*(-18)}`

`\frac{54+-\sqrt{54^(2) } }{-36}`

`(54+-54)/(-36)`

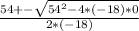
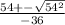
So, on one hand:

`x1=(54+54)/(-36)`

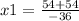
x1=-3

On the other hand:

`x2=(54-54)/(-36)`

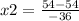
x2= 0

As you get the value of two zeros, and being a quadratic function it can have only 2 zeros, it means that -3 and 0 have multiplicity 1. These zeros can be seen in the graphic of the image.

So, the factored equation is -18*x*(x-3)

Second method

It consists of factoring the function. For that you do a common factor on the left side of the function, because on the right side, having zero value, this is not necessary.

For that, notice that in both terms the negative, the x with degree 1, and the 18 (54 is a multiple of 18, which is obtained by multiplying 18 by 3) appears. Then those can be taken as a common factor, leaving:

-18*x*(x+3)

Note that it is the same factored expression obtained earlier. Therefore, you can say that the zeros of the function are 0 and -3 with multiplicity 1.