Answer:
Heat transfer rate = 20.08 W
Step-by-step explanation:
Given that
D= 1 cm
K= 380 W/m.°C
Wall temperature = 200°C
Surrounding temperature = 30°C
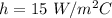
Rod is long so this is the case of long fin .
Heat transfer in long fin given as
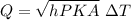
Here
P= π D
P = 3.14 x 0.01 m
P= 0.0314 m
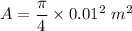
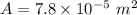
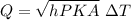
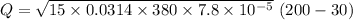
Q=20.08 W
So heat transfer rate = 20.08 W