Question

A delicate telescope mirror and support that can be modelled as a mass-spring system with mass of 12 kg and support stiffness of 10,000 N/m and a damping ratio of 0.08 is set into motion with an initial displacement of 8 mm and initial velocity of 1 mm/s. Determine: The damped natural frequency of the system

Answer 1

damping natural frequency = 28.76 rad/s

Step-by-step explanation:

given data

mass = 12 kg

stiffness = 10000 n/m

damping ratio = 0.08

displacement = 8 mm

initial velocity = 1 mm

to find out

damped natural frequency of the system

solution

we first find the natural frequency that is express as

natural frequency ω =
`\sqrt{(k)/(m) }` ..............1

here k is stiffness and m is mass

so ω =
`\sqrt{(10000)/(12) }`

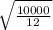
ω = 28.86 rad/s

so

damping frequency will be

damping frequency = ω ×
`√(1- r^2)` .....................2

here r is damping ration

damping frequency = 28.86 ×
`√(1- 0.08^2)`

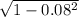
damping natural frequency = 28.76 rad/s