Question

: Show that the propositions (p ∨ q) ∧ (¬p ∨ r) and (p ∧ r) ⊕ (¬p ∧ q) are logically equivalent.

Answer 1

`(p\vee q)\wedge(\\eg p\vee r)\equiv(p\wedge r)\vee(\\eg p\wedge q)`

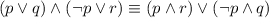
Step-by-step explanation:

The statements are logically equivalent if they have the same truth tables. So let´s use truth tables in order to determine if they are logically equivalent or not:

The picture that I attached you shows the truth table for each case. As you can see in the highlight columns:

`(p\vee q)\wedge(\\eg p\vee r)\equiv(p\wedge r)\vee(\\eg p\wedge q)`

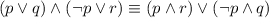
They are logically equivalent because they have exactly the same truth values between each other. Hence, we can conclude that they are logically equivalent.