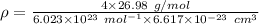Question

If the atomic radius of an FCC metal is 0.143nm and its atomic weight is 26.98 g/mol, 1. What is the length of its unit cell in nm and cm? 2. What is the volume in cubic nanometers and cubic centimeters? 3. What is the density of the metal in g/cc?

Answer 1

Edge length = 0.40446 nm =
`4.0446* 10^(-8)\ cm`

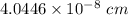
Volume = 0.06617 nm³ =
`6.617* 10^(-23)\ cm^3`

`\rho=2.708\ g/cm^3`

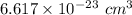
Step-by-step explanation:

Given that:

The radius = 0.143 nm

For FCC,

`Edge\ length=\frac {4}{\sqrt {2}}* radius`

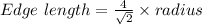
Thus,

`Edge\ length=\frac{4}{\sqrt {2}}* 0.143\ nm=2√(2)* \:0.143\ nm=0.40446\ nm`

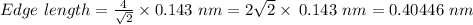
Edge length = 0.40446 nm

Also, 1 nm =
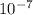`10^(-7)` cm

So,

Edge length =
`4.0446* 10^(-8)\ cm`

Volume =
`{(Edge\ length)}^3={0.40446}^3\ nm^3=0.06617\ nm^3`

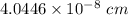
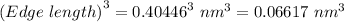
Volume = 0.06617 nm³

Also, 1 nm³ =
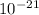`10^(-21)` cm³

Volume =
`6.617* 10^(-23)\ cm^3`

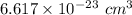
The expression for density is:

`\rho=\frac {Z* M}{N_a* {Volume}}`

`N_a=6.023* 10^(23)\ {mol}^(-1)`

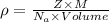
M is molar mass = 26.98 g/mol

For FCC , Z= 4

Thus,

`\rho=\frac {4* 26.98\ g/mol}{6.023* 10^(23)\ {mol}^(-1)* 6.617* 10^(-23)\ cm^3}`

`\rho=\frac {107.92}{10^(-23)* \:10^(23)* \:6.023* \:6.617}\ g/cm^3`

`\rho=(107.92)/(39.854191)\ g/cm^3`

`\rho=2.708\ g/cm^3`