Answer:
Since, the equation of a line passes through
 with slope m is,
with slope m is,

Thus, the equation of line passes through (4, 3) with slope
 is,
is,
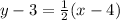
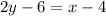
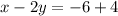

If x = 0,
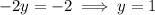
Thus, the line intersects y-axis at (0, 1),
If y = 0,
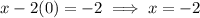
Thus, the line intersects x-axis at (-2, 0),
By joining the points (0, 1) and (-2, 0) we get the graph of the given line ( shown below )