Question

Show (analytically) with a few lines of math that the force exerted by a magnetic field does no work on a charged particle. Do this by showing that the rate of change of kinetic energy is zero. Your proof should be valid for arbitrary directions of v and B

Answer 1

We know that force on the moving (velocity V) charge q due to magnetic field B given as

`F=q(\vec{V}* \vec{B})`

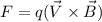
If force act for time t then energy gained by moving charge

`E=t(\vec{F}.\vec{V})`

`F=q(\vec{V}* \vec{B})`

`E=t(\vec{q(\vec{V}* \vec{B})}.\vec{V})`

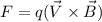
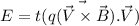
We know that

`For\ vector\ a\ and\ b\\ a.(\vec{a}* \vec{b})=0`

So

E=0

Now we can say that total kinetic energy of charge q will become

`K.E.=(1)/(2)mV^2+E`

`K.E.=(1)/(2)mV^2+t(\vec{F}.\vec{V})`

`K.E.=(1)/(2)mV^2`

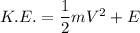
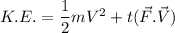
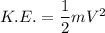
So

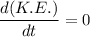`(d(K.E.))/(dt)=0` (V= constant)

We can say that

K.E.= constant

So the force exerted by a magnetic field does no work on a charged particle.