Answer:
A, C and D
Explanation:
Let us find the slope(rate of change ) of each pair of points
The slope formula is
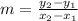
Plug in the points (− 4 ,− 11 ) and (-2 , − 7) to get;
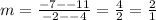
The rate of change of this pair 2:1
For B part, we plug the points ( 5 , 6 ) and ( − 5 , 12 )
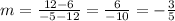
The rate of change is NOT 2:1
For part C, we plug in ( 0 , − 3 ) and ( − 4 , − 11 )
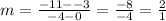
The rate of change of this pair is also 2:1
For part D, we plug in (0 , − 3) and ( 5 , 7 )
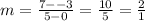
This also has rate of change to be 2:1