Question

A particle's position is defined by: x = 4t^3-27t^2+17t+8, where x is expressed in meters and t in seconds. Determine (a) the total distance traveled the 2nd time the velocity is zero and (b) the velocity when the acceleration is zero.

Answer 1

a)x = 100.56

b) t = 2.25 s

Step-by-step explanation:

given equation

x = 4 t³ - 27 t² + 17 t + 8

to get velocity we need to differentiate the expression w.r.t time

`(dx)/(dt)=(d)/(dt)(4 t^3- 27 t^2+ 17 t + 8)`

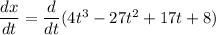
on solving the differential equation

v = 12 t² -54 t + 17

at v = 0

using quadratic equation to solve

we get

`t = \frac{-(-54)\pm \sqrtr{-54^2-4* 12* 17}}{2* 12}`

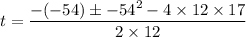
t = 4.16 s and 0.34 s

x = 4 × 4.16³ - 27 × 4.16² + 17 × 4.16 + 8

x = -100.56

x = 100.56

b) v = 12 t² -54 t + 17

to get acceleration we need to differentiate the expression w.r.t time

`(dv)/(dt)=(d)/(dt)(12 t^2- 54 t+ 17)`

on solving the differential equation

a = 24 t -54

time at which acceleration will be zero

24 t = 54

t = 2.25 s