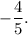Question

Consider the points A(3,−3), B(−2, 1), C(6, 0), and D(1, 4). Point A is joined to point B to create segment AB and point C is joined to point D to create segment CD.

Part A
a. What is the slope of AB?
b. What is the slope of CD?

Segments AB and CD are translated 2 units to the left to get segments A′B′ and C′D′.
Part B
a. What is the slope of A′B′?
b. What is the slope of C′D′?

Answer 1

Answer: The slopes of AB, CD, A'B' and C'D' are equal and is equal to
`-(4)/(5).`

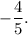
Step-by-step explanation: We are given the points A(3,−3), B(−2, 1), C(6, 0), and D(1, 4). Point A is joined to point B to create segment AB and point C is joined to point D to create segment CD.

We are given to answer the following two parts :

Part A : To find the slope of AB and CD.

We know that the slope of a line containing the points (a, b) and (c, d) is given by

`m=(d-b)/(c-a).`

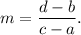
Therefore, the slopes of AB and CD are

`\textup{slope of AB}=(1-(-3))/(-2-3)=(4)/(-5)=-(4)/(5),\\\\\\\textup{slope of CD}=(4-0)/(1-6)=(4)/(-5)=-(4)/(5).`

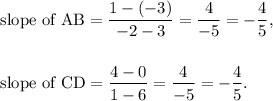
Part B: Segments AB and CD are translated 2 units to the left to get segments A′B′ and C′D′.

To find the slopes of A'B' and C'D'.

We know that, if a point (x, y) is translated 2 units to the left, then its co-ordinates becomes

(x, y) ⇒ (x-2, y).

So, the co-ordinates of A', B', C' and D' are

A(3, -3) ⇒ A'(3-2, -3) = (1, -3),

B(-2, 1) ⇒ B'(-2-2, 1) = (-4, 1),

C(6, 0) ⇒ C'(6-2, 0) = (4, 0),

D(1, 4) ⇒ D'(1-2, 4) = (-1, 4).

Therefore, the slopes of A'B' and C'D' are

`\textup{slope of A'B'}=(1-(-3))/(-4-1)=-(4)/(5),\\\\\\\textup{slope of C'D'}=(4-0)/(-1-4)=-(4)/(5).`

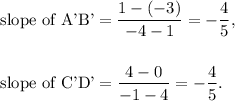
Thus, the slopes of AB, CD, A'B' and C'D' are equal and is equal to
`-(4)/(5).`

Answer 2

Part A:

a. The slope of AB is
`-(4)/(5)`

b. The slope of CD is
`-(4)/(5)`

Part B:

a. The slope of A'B' is
`-(4)/(5)`

b. The slope of C'D' is
`-(4)/(5)`

Explanation:

- The rule of a slope of a line whose endpoints are
`(x_(1),y_(1))`

and
`(x_(2),y_(2))` is
`m=(y_(2)-y_(1))/(x_(2)-x_(1))`

Part A:

∵ Point A = (3 , -3) and point B = (-2 , 1)

∵ Point C = (6 , 0) and point D = (1 , 4)

a.

∴
`m_(AB)=(1-(-3))/((-2)-3)=(1+3)/(-2-3)=(4)/(-5)`

∴ The slope of AB is
`-(4)/(5)`

b.

∴
`m_(CD)=(4-0)/(1-6)=(4)/(-5)`

∴ The slope of CD is
`-(4)/(5)`

- The image of point (x , y) by translation to the left k units is (x - k , y)

- Translation doesn't change the slope of a line, so the line and its

image have same slope

Part B:

∵ Segments AB and CD are translated 2 units to the left to get

segments A′B′ and C′D′

∵ Point A' = (3 - 2 , -3) and point B' = (-2 - 2 , 1)

∴ Point A' = (1 , -3) and point B' = (-4 , 1)

∵ Point C' = (6 - 2 , 0) and point D' = (1 - 2 , 4)

∴ Point C' = (4 , 0) and point D' = (-1 , 4)

a.

∴
`m_(A'B')=(1-(-3))/((-4)-1)=(1+3)/(-4-1)=(4)/(-5)`

∴ The slope of A'B' is
`-(4)/(5)`

b.

∴
`m_(C'D')=(4-0)/(-1-4)=(4)/(-5)`

∴ The slope of C'D' is
`-(4)/(5)`