Question

A water tank in the shape of an inverted cone has a height of 11 feet and a radius of 6.0 feet. Find the volume of the water tank when the water is 7 feet deep.

Answer 1

A water tank in the shape of an inverted cone has a height of 11 feet and a radius of 6.0 feet. The volume of water in a conical tank is 107 cubic feet.

Solution:

Consider the figure attached below as side view of inverted cone shape.

AG = BG = 6 feet [Radius ]

OG = 11 feet [water tanks height ]

OE = 7 feet [Depth of water ]

Need to calculate EC first , which is radius of uppermost surface till where the water is filled.

Consider triangle OEC and triangle OGB

Angle OEG = Angle OGB [both are 90^{\circ}]

Angle GOB = Angle EOC [Same angle]

So using Angle angle similarity criterion, it can be said that

Triangle OEC is similar to triangle OGB.

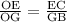`\frac{\mathrm{OE}}{\mathrm{O} \mathrm{G}}=\frac{\mathrm{EC}}{\mathrm{GB}}` [Ratio of corresponding side of similar triangles ]

`(7)/(11)=(E C)/(6)`

`\mathrm{EC}=(42)/(11) \text { feet }`

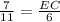
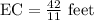
Volume of water = Volume of cone of height 7 feet and radius 42/11 feet

Formula for volume of cone =
`\pi r^(2) h=\pi *\left((42)/(11)\right)^(2) * (7)/(3)`

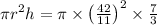
= 106.909 which is approximately 107

Hence volume of water in a conical tank is 107 cubic feet.