Question

An electron initially has a speed 16 km/s along the x-direction and enters an electric field of strength 27 mV/m that points in the y-direction and has a width of 22.5 cm. (a) How long does it take the electron to pass through the field? μs (b) How far is the deflection?

Answer 1

(a). The time is 14.0 μs.

(b). The deflection is 0.47 m.

Step-by-step explanation:

Given that,

Speed = 16 km/s

Electric field strength = 27 mV/m

Width = 22.5 cm

(a). We need to calculate the time

Using formula of velocity

`v=(d)/(t)`

`t=(d)/(v)`

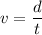
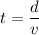
Put the value into the formula

`t=(22.5*10^(-2))/(16*10^(3))`

`t=0.0000140625\ sec`

`t=14.0*10^(-6)\ sec`

`t=14.0\ \mu\ s`

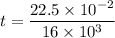
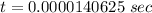
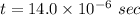
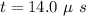
(b). We need to calculate the deflection

Using equation of motion

`s=ut+(1)/(2)at^2`

`s=0+(1)/(2)*(qE)/(m)* t^2`

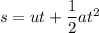
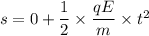
Here, s = deflection

q = charge of electron

m = mass of electron

Put the value in the equation

`s=(1)/(2)*(1.6*10^(-19)*27*10^(-3))/(9.1*10^(-31))*(14.0*10^(-6))^2`

`s=0.47\ m`

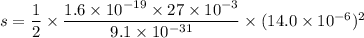
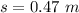
Hence, (a). The time is 14.0 μs.

(b). The deflection is 0.47 m.

Answer 2

a)
`t=1.4* 10^(-5)\ s`

b)S= 46.4 cm

Step-by-step explanation:

Given that

Velocity = 16 Km/s

V= 16,000 m/s

E= 27 mV/m

E=0.027 V/m

d= 22.5 cm

d= 0.225 m

a)

lets time taken by electron is t

d = V x t

0.225 = 16,000 t

`t=1.4* 10^(-5)\ s`

b)

We know that

F = m a = E q ------------1

Mass of electron ,m

`m=9.1* 10^(-31)\ kg`

Charge on electron

`q=1.6* 10^(-19)\ C`

So now by putting the values in equation 1

`a=(E q)/(m)`

`a=(1.6* 10^(-19)* 0.027)/(9.1* 10^(-31))\ m/s^2`

`a=4.74* 10^(9)\ m/s^2`

`S= ut+(1)/(2)at^2`

Here initial velocity u= 0 m/s

`S= (1)/(2)* 4.74* 10^(9)* (1.4* 10^(-5))^2\ m`

S=0.464 m

S= 46.4 cm

S is the deflection of electron.