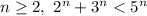Question

Use induction on n to prove that fir all n>=2, 2^n+3^n<5^n

Answer 1

Step-by-step explanation:

We first prove the base case, which is proving that the inequality holds for n=2:

`2^2+3^2=4+9=13<25=5^2`

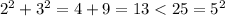
So
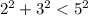`2^2+3^2 < 5^2` and base case is proven.

We then do the inductive step, which is assuming that the inequality holds for n=k, and proving out of that that the inequality also holds for n=k+1:

Assume the inequality holds for n=k. This means that

`2^k+3^k<5^k`

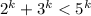
Our goal is then to show that
`2^(k+1)+3^(k+1)<5^(k+1)`.

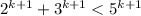We have that

`2^(k+1)+3^(k+1)=2\cdot 2^k+3\cdot 3^k<3\cdot 2^k+3\cdot 3^k =3\cdot (2^k+3^k)<3\cdot 5^k < 5\cdot 5^k = 5^(k+1)`

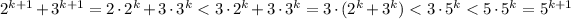
(since we're assuming that
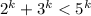`2^k+3^k<5^k`, we know that
`3\cdot (2^k+3^k)<3\cdot 5^k` ).

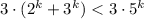So
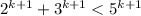`2^(k+1)+3^(k+1)<5^(k+1)`, and the inductive step is proven.

Therefore we can conclude by the principle of mathematical induction that for all
`n \geq 2,~2^n+3^n<5^n`