Question

A tuning fork generates sound waves with a frequency of 240 Hz. The waves travel in opposite directions along a hallway, are reflected by walls, and return. The hallway is 46.0 m long and the tuning fork is located 14.0 m from one end. What is the phase difference between the reflected waves(in degrees) when they meet at the tuning fork? The speed of sound in air is 343 m/s. [answer 68.2°] Pls show steps

Answer 1

The phase difference between the reflected waves when they meet at the tuning fork is 159.29 rad.

Step-by-step explanation:

Given that,

Frequency of sound wave = 240 Hz

Distance = 46.0 m

Distance of fork = 14 .0 m

We need to calculate the path difference

Using formula of path difference

`\Delta x=2(L_(2)-L_(1))`

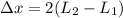
Put the value into the formula

`\Delta x =2((46.0-14.0)-14.0)`

`\Delta x=36\ m`

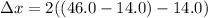
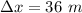
We need to calculate the wavelength

Using formula of wavelength

`\lambda=(v)/(f)`

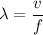
Put the value into the formula

`\lambda=(343)/(240)`

`\lambda=1.42\ m`

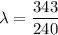
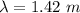
We need to calculate the phase difference

Using formula of the phase difference

`\phi=(2\pi)/(\lambda)* \delta x`

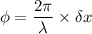
Put the value into the formula

`\phi=(2\pi)/(1.42)*36`

`\phi=159.29\ rad`

`\phi\approx 68.2^(\circ)`

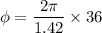
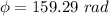
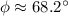
Hence, The phase difference between the reflected waves when they meet at the tuning fork is 159.29 rad.