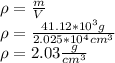Answer:


Step-by-step explanation:
By the Archimedes principle we know that every body submerged in a fluid is buoyed up by a force equal to the weight of the fluid displaced by the object.
Due to this, the object has a loss weight when immersed in alcohol of:

So, we can find the displaced mass of alcohol:
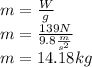
Now, we calculate the displaced volume of alcohol, which is the same volume of the object:
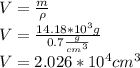
Object mass is:
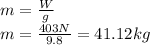
Finally, we can find the density of the object: