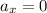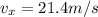Answer:
A.
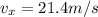
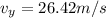
B.
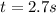
C.
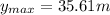
D.
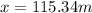
E.
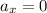
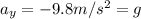
F.
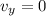
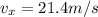
Step-by-step explanation:
From the exercise our initial values are:

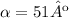
A. The horizontal and vertical components are:
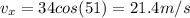
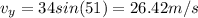
B. At maximum height the y-component of velocity becomes 0
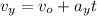
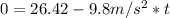
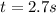
C. The maximum height above the ground is:
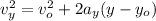
At maximum height the y-component of velocity becomes 0
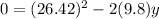
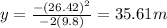
D. To find how dar from its firing point does the sell land we need to calculate how much time does it take to do it first
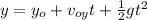
When the shell land y=0
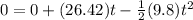
Solving the quadratic equation for t
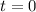 or
or
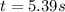
Since time can not be 0 t=5.39s
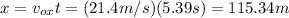
E. Since the velocity at the horizontal component is constant
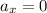
The vertical acceleration of the shell is gravity
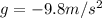
F. At highest point the vertical component is 0. The shell stops going up ans start to go down
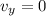
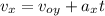
Since