Question

What must be the distance (in meters) between a point charge q1 = 16 μC and a point charge q2 = 32 μC for the electrostatic force between them to have a magnitude of 9 newtons?

Answer 1

d = 0.71 meters

Step-by-step explanation:

It is given that,

Charge 1,
`q_1=16\ \mu C=16* 10^(-6)\ C`

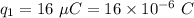
Charge 2,
`q_2=32\ \mu C=32* 10^(-6)\ C`

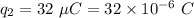
Electrostatic force between charges, F = 9 N

Let d is the distance between the charges. The electrostatic force between the charges is given by the product of charges and divided by square of distance between them. Mathematically, it is given by :

`F=k(q_1q_2)/(d^2)`

`d=\sqrt{(kq_1q_2)/(F)}`

`d=\sqrt{(9* 10^9* 16* 10^(-6)* 32* 10^(-6))/(9)}`

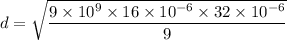
d = 0.71 meters

So, the distance between the charges is 0.71 meters. Hence, this is the required solution.