Answer:
Step-by-step explanation:
Given
First bicycle travels 6.10 km due to east in 0.21 h
Suppose its position vector is
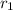
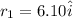
After that it travels 11.30 km at
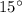 east of north in 0.560 h
east of north in 0.560 h
suppose its position vector is
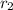
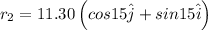
after that he finally travel 6.10 km due to east in 0.21 h
suppose its position vector is
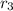
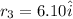
so position of final position is given by
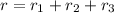

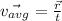
t=0.21+0.56+0.21=0.98 h
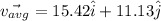
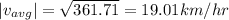
For direction

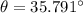 w.r.t to x axis
w.r.t to x axis