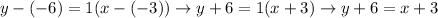Explanation:
The point-slpe form of an equation of a line:
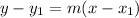
m - slope
(x₁, y₁) - point on a line
The formula of a slope:
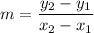
(x₁, y₁), (x₂, y₂) - points on a line
We have the points (3, 0) and (-3, -6).
Calculate the slope:
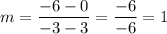
Put the value of the slope and the coordinates of the point (3, 0) or (03, 06) to the equation of a line:
FOR (3, 0):
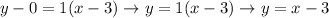
FOR (-3, -6):