Question

You received a shipment 20 days ago of 131I for treatment of hyperthyroidism. What fraction of the original shipment would you still have with a half-life of 8.040 days for I?

Answer 1

`(N(t))/(N_(0))=0.17830731692</p><p>`

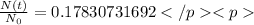
Step-by-step explanation:

There are many formulas that can describe the exponential decay of a substance. For example, one of the formulas we could use for the quantity that still remains after a time t, given an original quantity
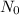`N_0` and a half-life of
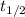`t_(1/2)` is:

`N(t)=N_(0)((1)/(2))^{t/t_(1/2)}`

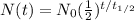
We want to calculate what fraction of the original shipment would still we have, that is,
`(N(t))/(N_(0))`

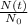
This is why it is useful to use the formula already written, now we can just calculate:

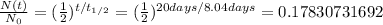`(N(t))/(N_(0))=((1)/(2))^{t/t_(1/2)}=((1)/(2))^(20days/8.04days)=0.17830731692`, which means that around 17.83% of the original substance has not decayed yet.