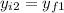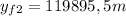Answer:
(a)
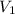 = 3910
= 3910
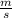
(b)
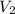 = 5181
= 5181
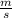
(c)
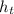 = 2762955 m
= 2762955 m
Step-by-step explanation:
Using equations of uniformly accelerated motion:
Equations:
-
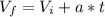
-
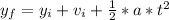
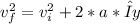
(a) Using equation 1:
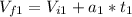 ⇒
⇒
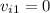 Because it upward from rest
Because it upward from rest
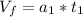
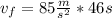
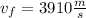
(b) Using equation 1:
 ⇒
⇒
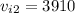 Because is the is the initial speed in the movement before changing acceleration
Because is the is the initial speed in the movement before changing acceleration
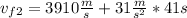
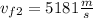
(c) Using equation 2:
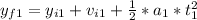 ⇒
⇒
 and
and
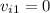 Because it upward from rest
Because it upward from rest


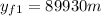
 ⇒
⇒