Question

A speedboat is approaching a dock at 25 m/s (56 mph). When the dock is 150 m away, the driver begins to slow down. a) What acceleration must the boat have to come to a stop just as it arrives at the dock? b) If the braking acceleration of the boat has a maximum magnitude of 1.0 m/s^2-, how fast is the boat going when it hits the dock? Convert your result to mph. c) If the braking acceleration of the boat has a maximum magnitude of 1.0 m/s^2, at what distance from the dock should the driver have begun slowing down?

Answer 1

a) -2.038 m/s²

b) 40.33 mph

c) 312.5 m

Step-by-step explanation:

t = Time taken

u = Initial velocity

v = Final velocity

s = Displacement

a = Acceleration

`v^2-u^2=2as\\\Rightarrow a=(v^2-u^2)/(2s)\\\Rightarrow a=(0^2-25^2)/(2* 150)\\\Rightarrow a=-2.083\ m/s^2`

Acceleration of the boat is -2.083 m/s² if the boat will stop at 150 m.

`v^2-u^2=2as\\\Rightarrow v=√(2as+u^2)\\\Rightarrow v=√(2* -1* 150+25^2)\\\Rightarrow v=18.03\ m/s`

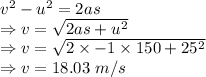
Speed of the boat by when it will hit the dock is 18.03 m/s

Converting to mph

`1\ mile=1609.34\ m`

`1\ h=3600\ seconds`

`18.03* (3600)/(1609.34)=40.33\ mph`

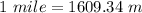
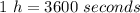
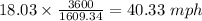
Speed of the boat by when it will hit the dock is 40.33 mph

`v^2-u^2=2as\\\Rightarrow s=(v^2-u^2)/(2a)\\\Rightarrow s=(0^2-25^2)/(2* -1)\\\Rightarrow s=312.5\ m`

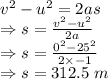
The distance at which the boat will have to start decelerating is 312.5 m