Question

An ant is crawling along a yardstick that is pointed with the 0-inch mark to the east and the 36-inch mark to the west. It starts at the 16 inch mark, crawls to the 29-inch mark, then moves to the 14-inch mark. What is the total distance the ant traveled? What was the total displacement of the ant?

Answer 1

• The total distance traveled is 28 inches.
• The displacement is 2 inches to the east.

Step-by-step explanation:

Lets put a frame of reference in the problem. Starting the frame of reference at the point with the 0-inch mark, and making the unit vector
`\hat{i}` pointing in the west direction, the ant start at position

`\vec{r}_0 = 16 \ inch \ \hat{i}`

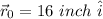
Then, moves to

`\vec{r}_1 = 29 \ inch \ \hat{i}`

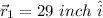
so, the distance traveled here is

`d_1 = |\vec{r}_1 - \vec{r}_0  | = | 29 \ inch   \ \hat{i} - 16 \ inch   \ \hat{i}  |`

`d_1 =  | 13 \ inch   \ \hat{i}  |`

`d_1 =  13 \ inch`

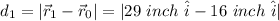
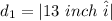
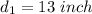
after this, the ant travels to

`\vec{r}_2 = 14 \ inch \ \hat{i}`

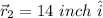
so, the distance traveled here is

`d_2 = |\vec{r}_2 - \vec{r}_1  | = | 14 \ inch   \ \hat{i} - 29 \ inch   \ \hat{i}  |`

`d_2 =  | - 15 \ inch   \ \hat{i}  |`

`d_2 =  15 \ inch`

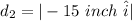
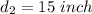
The total distance traveled will be:

`d_1 + d_2 = 13 \ inch + 15 \ inch = 28 \ inch`

The displacement is the final position vector minus the initial position vector:

`\vec{D}=\vec{r}_2 - \vec{r}_1`

`\vec{D}= 14 \ inch   \ \hat{i} - 16 \ inch \ \hat{i}`

`\vec{D}= - 2 \ inch \ \hat{i}`

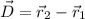
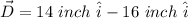
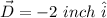
This is 2 inches to the east.