Answer:r=12.02 cm
Step-by-step explanation:
Given
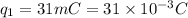
Placed at x=8 cm
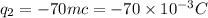
placed at a distance, suppose r
Electric field due to positive charge will be away from the origin and electric field due to negative charge is towards the origin
Thus net effect will be zero
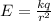
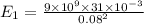
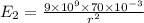
Equate
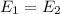
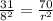
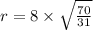
r=12.02 cm