Step-by-step explanation:
It is given that,
Height above which the stone was thrown, h = 10 m
Initial velocity of the stone, u = 8 m/s
Angle above the horizontal,
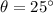
The horizontal component of velocity is,
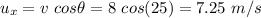
The vertical component of velocity is,
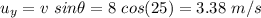
Let t is the time of flight in vertical motion. The second equation of motion is :
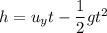
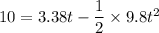
t = 0.34 seconds
Let s is the range of the stone. It can be calculated as :
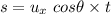
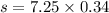
s = 2.46 meters
So, the range of the stone is 2.46 meters. Hence, this is the required solution.