Question

A nonconducting solid sphere of radius 8.40 cm has a uniform volume charge density. The magnitude of the electric field at 16.8 cm from the sphere's center is 2.04 x 103 N/C. (a) What is the sphere's volume charge density?

Answer 1

The sphere's volume charge density is 2.58 μC/m³.

Step-by-step explanation:

Given that,

Radius of sphere R= 8.40 cm

Electric field
`E= 2.04*10^(3)\ N/C`

Distance r= 16.8 cm

We need to calculate the sphere's volume charge density

Using Gauss's law

`\int{\vec{E}\cdot\vec{da}}=(Q_(enc))/(\epsilon_(0))`

`E* 4\pi r^2=(1)/(\epsilon_(0))*(4)/(3)\piR^3\rho`

`E=(\rho R^3)/(3\epsilon_(0)r^2)`

`\rho=(3* E*\epsilon_(0)r^2)/(R^3)`

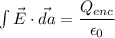
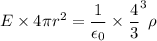
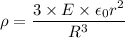
Put the value into the formula

`\rho=(3*2.04*10^(3)*8.85*10^(-12)*(16.8*10^(-2))^2)/((8.40*10^(-2))^3)`

`\rho=2.58*10^(-6)\ C/m^3`

`\rho=2.58\ \mu C/m^3`

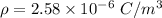
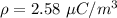
Hence, The sphere's volume charge density is 2.58 μC/m³.