Answer:
The function t(h) is t(h) =

The time to reach a height 250 feet is 4.68 seconds
Explanation:
* Lets explain how to solve this problem
- An object dropped from a height of 600 feet has a height, h(t), in feet
after t seconds have elapsed, such that
h(t) = 600 − 16 t²
- We need to express t is a function of the height h
- To do that lets find t in terms of h
∵ h = 600 - 16 t²
- Add 16 t² to both sides
∴ 16 t² + h = 600
- Subtract h from both sides
∴ 16 t² = 600 - h
- Divide both sides by 16
∴ t² =
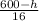
- Take √ for both sides
∴ t =

∴ t(h) =

* The function t(h) is t(h) =

- Now lets find the time of the object to reach a height 250 feet
∵ t(h) =

∵ h = 250
∴ t(250) =
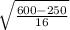
∴ t(250) = 4.68 seconds
* The time to reach a height 250 feet is 4.68 seconds