Question

The function f(x) = -(x-20)(x - 100) represents a company's monthly profit as a function of x, the number of purchase

orders received. Which number of purchase orders will generate the greatest profit?
20
60
Mark this and return
Save and Exit
Next
Submit

Answer 1

The number of purchase orders that will generate the greatest profit is 60 orders

Explanation:

we have

`f(x)=-(x-20)(x-100)`

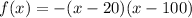
This is a vertical parabola open downward

The vertex is a maximum

The y-coordinate of the vertex represent the greatest profit

The x-coordinate of the vertex represent the number of purchase orders for the greatest profit

Convert the function in vertex form

`f(x)=-(x-20)(x-100)`

`f(x)=-(x^2-100x-20x+2,000)`

`f(x)=-(x^2-120x+2,000)`

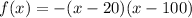
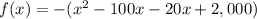
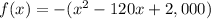
Complete the square

`f(x)=-(x^2-120x)-2,000`

`f(x)=-(x^2-120x+3,600)-2,000+3,600`

`f(x)=-(x^2-120x+3,600)+1,600`

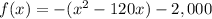
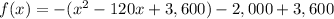
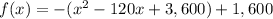
Rewrite as perfect squares

`f(x)=-(x-60)^2+1,600`

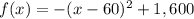
The vertex is the the point (60,1,600)

therefore

The greatest profit is $1,600

The number of purchase orders that will generate the greatest profit is 60 orders