Question

Quinn is building an enclosed pen in his backyard he wants the perimeter to be no more than 50 feet he also wants the length to be at least 5 feet longer than the width

Answer 1

Option B width = 5 feet and length = 12 feet

The solution in the attached figure

Explanation:

The options of the questions are

Which combination of width and length will meet Quinn’s requirements for the pen?

A. width = 7 feet and length = 20 feet

B. width = 5 feet and length = 12 feet

C. width = 15 feet and length = 10 feet

D. width = 11 feet and length = 15 feet

Let

x -----> the length of the enclosed pen in feet

y-----> the width of the enclosed pen in feet

we know that

The perimeter is equal to

`P=2(x+y)`

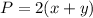
In this problem

`2(x+y)\leq 50`

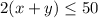
Simplify

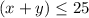`(x+y)\leq 25` ----> inequality A

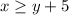`x\geq y+5` ---> inequality B

using a graphing tool

The solution is the triangular shaded area

see the attached figure N 1

Remember that

The values of x and y cannot be a negative number

If a ordered pair is a solution of the system of inequalities, then the ordered pair must satisfy both inequality

Verify each case

case A) width = 7 feet and length = 20 feet

so

For y=7, x=20

Check inequality A

`(20+7)\leq 25`

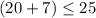
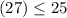`(27)\leq 25` ----> is not true

therefore

This combination of width and length will not meet Quinn’s requirements for the pen

case B) width = 5 feet and length = 12 feet

so

For y=5, x=12

Check inequality A

`(12+5)\leq 25`

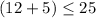
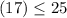`(17)\leq 25` ----> is true

Check inequality B

`12\geq 5+5`

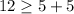
`12\geq 10` -----> is true

therefore

This combination of width and length will meet Quinn’s requirements for the pen

case C) width = 15 feet and length = 10 feet

so

For y=15, x=10

Check inequality A

`(10+15)\leq 25`

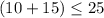
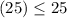`(25)\leq 25` ----> is true

Check inequality B

`10\geq 15+5`

`10\geq 20` -----> is not true

therefore

This combination of width and length will not meet Quinn’s requirements for the pen

case D) width = 11 feet and length = 15 feet

so

For y=11, x=15

Check inequality A

`(15+11)\leq 25`

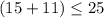
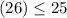`(26)\leq 25` ----> is not true

therefore

This combination of width and length will not meet Quinn’s requirements for the pen

Note If the ordered pair is a solution of the system of inequalities, then the ordered pair must lie on the shaded area

see the attached figure N 2 to better understand the problem