Step-by-step explanation:
Given that,
Initial velocity = 19.7 m/s
Angle = 45°
(a). We need to calculate the velocity at the top of the trajectory
Using formula of velocity at the top of the trajectory
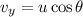
Put the value into the formula


The top of the trajectory is 13.93 m/s.
(b). We need to calculate the maximum height
Using formula of height
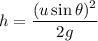
Put the value into the formula
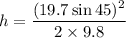
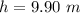
The maximum height is 9.90 m.
(c). We need to calculate the range
Using formula of range

Put the value into the formula
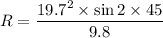

The range is 39.6 m.
(d). We need to calculate the time
Using formula of time
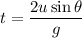
Put the value in to the formula
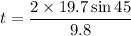
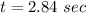
The time is 2.84 sec.
Hence, This is the required solution.