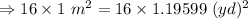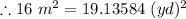Question

16 square meters is equivalent to how many square yards?

a.
177.8 square yards

b.
20 square yards

c.
12.8 square yards

d.
1.4 square yards

Answer 1

b.
`16 \ m^(2)=19.13584 \ (y d)^(2) \approx \bold{20 \ (y d)^(2)}`

Given:

16 square meters

Solution:

The square meter and the square yards conversion is:

`1 \ m^(2)=1.19599 \ (y d)^(2)`

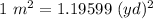
The “square meter” is the unit of the area which is equal to the square with the one meter as its side.

The “square yard” is also a unit of area which is equal to the square with the one yard as its side.

Now, from the question,

`\Rightarrow 16 * 1 \ m^(2)=16 * 1.19599 \ (y d)^(2)`

`\therefore 16 \ m^(2)=19.13584 \ (y d)^(2)`

Answer 2

1 square meter = 1.196 square yards.

Multiple total square meters by 1.196:

16 x 1.196 = 19.134

The closest answer is b. 20 square yards.