Question

Consider a disk of radius 4.9 cm with a uni- formly distributed charge of +5.6 (C. Compute the magnitude of the electric field at a point on the axis and 3 mm from the center. The value of the Coulomb constant is 8.98774 x 10 N m2/C2

Answer 1

`E=1.27* 10^(12)\ N/C`

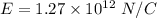
Step-by-step explanation:

Given that,

Radius of the disk, r = 4.9 cm = 0.049 m

Charge, q = +5.6 C

We need to find the the electric field at a point on the axis and 3 mm from the center, x = 0.003 m

At a point on the axis of a ring, the electric field is given by :

`E=(kqx)/((x^2+r^2)^(3/2))`

`E=(9* 10^9* 5.6* 0.003)/((0.003^2+0.049^2)^(3/2))`

`E=1.27* 10^(12)\ N/C`

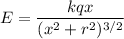
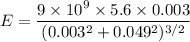
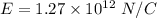
So, the electric field at a point on the axis is
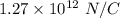`1.27* 10^(12)\ N/C`. Hence, this is the required solution.