Answer:
The lesser number of workbooks are 1,000
Explanation:
The correct question is
The profit P (in thousands of dollars) for an educational publisher can be modeled by P=-b³+5b²+b where b is the number of workbooks printed (in thousands). Currently, the publisher prints 5000 workbooks and makes a profit of $5000. What lesser number of workbooks could the publisher print and still yield the same profit?
we have
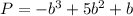
For
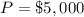
substitute in the equation and solve for b
Remember that the profit and the number of workbooks is in thousands
so
P=5
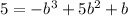
Using a graphing tool
Solve the cubic function
The solutions are
x=-1
x=1
x=5
therefore
The lesser number of workbooks are 1,000
Verify
For b=1
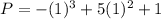
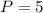 -----> is in thousands
-----> is in thousands
so
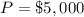 ----> is ok
----> is ok