Answer:
1) The maximum jump height is reached at A.

2) The maximum center of mass height off of the ground is B.
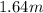
3) The time of flight is C.
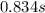
4) The distance of jump is B.
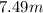
Step-by-step explanation:
First of all we need to decompose velocity in its rectangular components, so
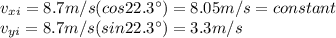
1) We use,
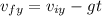 , as we clear it for
, as we clear it for
 and using the fact that
and using the fact that
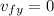 at max height, we obtain
at max height, we obtain
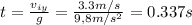
2) We can use the formula
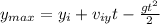 for
for
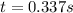 , so
, so

3) We can use the formula
 , to find total time of fligth, so
, to find total time of fligth, so
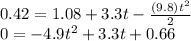 , as it is a second-grade polynomial, we find that its positive root is
, as it is a second-grade polynomial, we find that its positive root is

4) Finally, we use
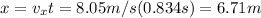 , as it has an additional displacement of
, as it has an additional displacement of
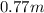 due the leg extension we obtain,
due the leg extension we obtain,
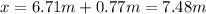 , aprox
, aprox
